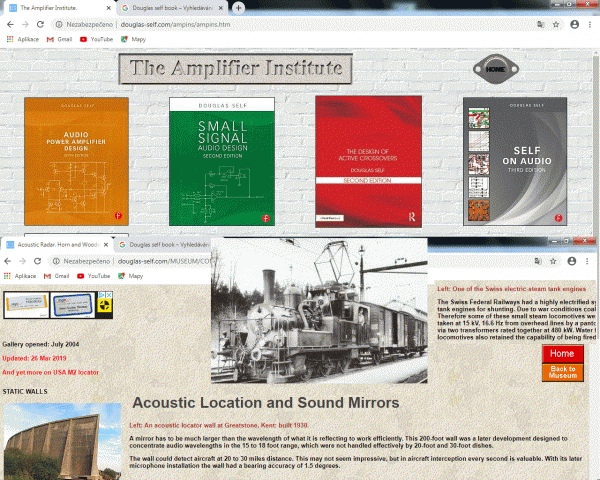
U Douglase Selfa, autora publikací věnovaných audiotechnice a zesilovačům, jsem taky kdysi objevil ty akustické lokátory a největší zvukové paraboly na světě. Tato betonová zvuková zrcadla byla postavena na břehu kanálu La Manche.
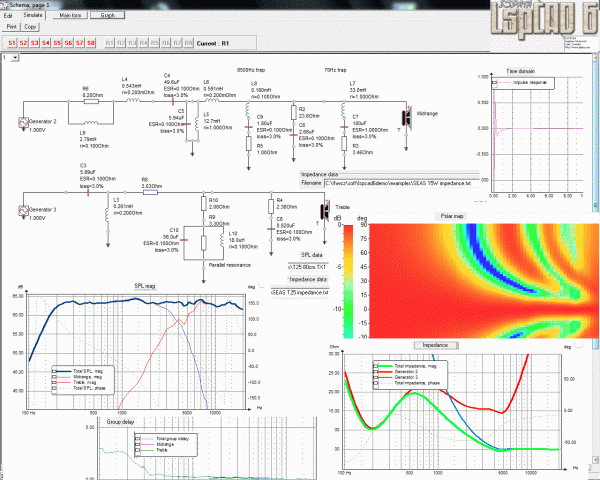
Ale opět se vrátíme k výhybkám, ať se ten Zobel Network nějak dořeší. V poslední verzi LspCAD6 se postupně ladí pasivní výhybky až do výsledného schématu, který se opravdu hodně vzdálil původní představě horní, dolní a pásmové propusti. A v examples jsou stále k dispozici odměřená data měničů, jen už jsou vedeny jako obyčejný textový soubor *.txt a ne jako dřív *.zma a *.frd.
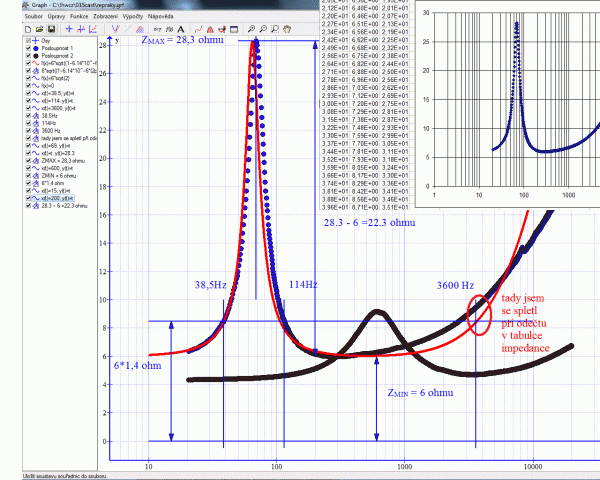
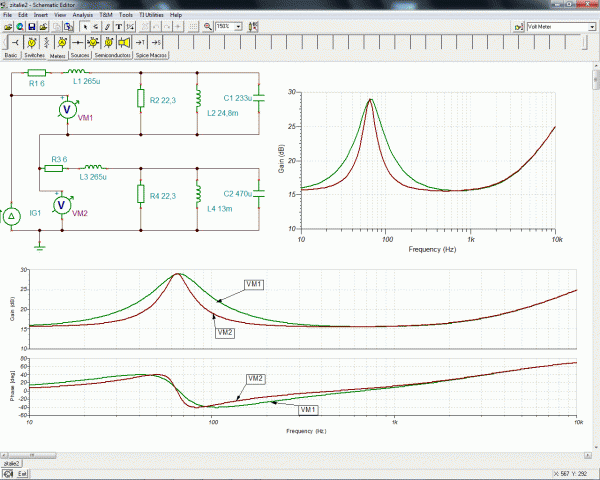
Znovu jsem zkusil přes převod textového souboru Excelem do programu Graph vložit textové posloupnosti *.txt impedancí obou reproduktorů a máte je uložené jako *.xls v přílohách pod článkem. Pak jsem známým způsobem, že při mezním kmitočtu má diagram tvar čtverce z rovnosti minimální odporu (6 ohmů) vynásobeného odmocninou ze dvou (úhlopříčka) čtverce (6*1,4=8,5) určil tři kmitočty a z nich pak dle rovnic 2pifL=8,5 a 1/(2pifC)=8,5 i náhradní parametry modelu reproduktoru, tj. přepočítanou indukčnost (hmotnost) 24,8mH, kapacitu (podajnost) 233uF a indukčnost kmitací cívky 265uH. Odpor (tlumení) mechanické rezonance se určí prostým odečtem odporu vinutí a maxima pří rezonancí (28.3-6 =22,3 ohmu).
Metoda mého modelu vychází z předpokladu, že reproduktor se pří nízkých kmitočtech chová jako odpor vinutí, pak se impedance zvyšuje díky přepočítané indukčnosti rezonančního obvodu. Následuje špička rezonance a pak dochází ke zkratu kapacitou rezonančního obvodu. Pak by měla být chvíli charakteristika rovná než se začne uplatňovat reaktance kmitací cívky. Následovat by měla další rezonance tentokrát s mezizávitovou kapacitou kmitačky a následný pád dolů, protože každá součástka se nakonec chová jako kondenzátor. Všimněte si jak elegantně lze parametrickým zadáním průběhu funkce v programu Graph kótovat, či kreslit pomocné osy a kombinovat posloupnosti bodů x/y. A navíc podle potřeby lze zobrazované části vypínat zatržítky ve čtvereččích v levém menu.
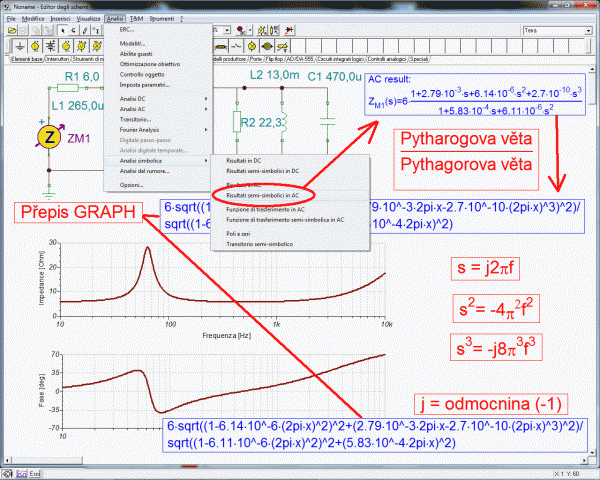
Tady jsem se hodně zdržel. Předpoklad, že lze brát jednotlivé prvky postupně za sebou, zde neplatí, protože rezonanční špička je příliš úzká. Takže jsem sice trefil rezonanční kmitočet, ale oproti tabulce vyšla rezonanční křivka širší. Takže zkusmo jsem měnil L a současně C tak, aby rezonanční kmitočet podle Thomsonova vztahu (2pfL = 1/(2pifC)) zůstal. Nakonec úzkou rezonanční charakteristiku vystihlo zmenšení indukčnosti na polovinu a zvětšení kapacity na dvojnásobek (kontrolováno kurzorem v grafu pro kmitočty 38,5 a 114 Hz). Hodnoty byly zaokrouhleny tak, aby se rezonance doladila do shody s tabulkou. Následovala symbolická analýza, která dá zlomek automatizační přenosové funkce. Časové konstanty jsme z ní minule přepsali do bloku přenosové funkce programu Multisimu. Tentokrát jsem se rozhodl, že zkusím vypočítat velikost komplexního čísla v čitateli i ve jmenovateli podle Pythagorovy věta (velikost = odmocnina (Re*Re+Im*Im)). S použitím červených rámečků pro mocniny operátorů s v obrázku jsem to po několika chybách přepsal do zápisu pro vykreslení v programu GRAPH, viz výše. Shoda je téměř dokonalá s výjimkou chybného odečtu posledního mezního kmitočtu v tabulce impedance (3600 Hz) a rychlejším stoupáním grafu na konci charakteristiky. To ale půjde doladit, protože se zde pravděpodobně začíná uplatňovat mezizávitová kapacita cívky, která indukční nárůst impedance zpomaluje. U výškového reproduktoru by mělo bý určení náhradních parametrů jednodušší, protože rezonanční křivka je širší (jakost rezonančního obvodu menší). Jsem spokojen, pokud někdo zkoušel v Excelu vložit spojnici trendu, tak ví, že proložit spojnicí trendu závislost s takhle ostrým lomem je i polynomem vyššího řádu nemožné.
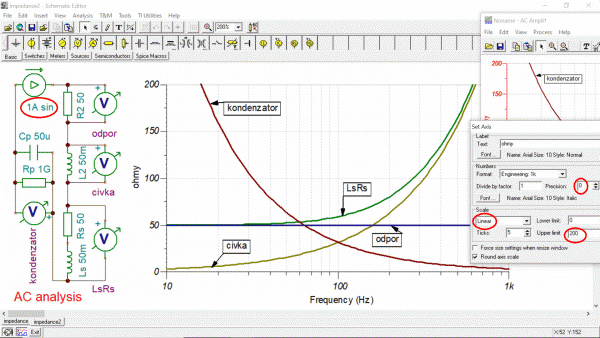
Protože jsem začal nepedagogicky složitým zapojením na začátek, napravím to. U ideální cívky s kmitočtem lineárně narůstá reaktance (2pifL). TinaPro má virtuální měřič impedance značený buď Z neb Ohm. Dají se nastavit i lineární osy. Měřič impedance může být v zapojení ale jen jeden. Pokud chceme současně zobrazit několik impedancí současně, je nutné aplikovat Ohmův zákon a jako vstup použít rozmítaný zdroj proudu 1A a napětí na impedancích měřit voltmetry. Myslel jsem, že virtuální ohmetr měří stejně, ale není tomu tak.
Takže se zapojí jeden kmitočtově rozmítaný zdroj proudu a voltmetry na několika typických impedancích (R,L,C, RsLs a RpCp s Rp blízké nekonečnu). Je použita vodorovná logaritmická osa a lineární svislá. To zkreslí přímku přímé úměry u reaktance cívky takže vypadá podobně jako nepřímá reaktance kondenzátoru s kmitočtem (1/(2pifC)). U cívky s odporem vinutí 50 ohmů se při nízkých kmitčtech cívka chová jako odpor vinutí a od mezního kmitočtu (opět fázorák ve tvaru čtverce 2pifL = R) převáží reaktance cívky (zelená křivka). Pozor, nelze sečítat přímo křivky v grafu, ale je zapotřebí jít přes Pythagorovu větu (fázový posuv 90°). A na závěr přikládám původní a upravenou charakteristiku reproduktoru. Nechal jsem na ose decibely, protože v tomto případě to vypadá podobně (30dB je 30krát).
No a samozřejmě, že každé zapojení lze vylepšovat a to platí i pro generátor s diakem. Jednak se na osciloskopu ukázalo, že staré BKáčko vytažené ze sklepa v záporném zdroji kmitá (stačilo připojit externě kondenzátor) a jednak, že kdyby člověk přemýšlel, tak není třeba převracet obrazovku osciloskopu, ale stačí přepólovat napájecí zdroj.
A na závěr, Myšákovi se tentokrát nezdá úprava strojového kompexního vztahu symbolické analýzy. Je přesvědčen, že analytické řešení součtu impedance R+j2pifL s admitancí 1/(1/R+j2pfC+1/(j2pifL)) dá po roznásobení komplexně sdruženým číslem mnohem elegantnější výsledek a má pravdu. Nicméně uznává, že po další úpravě připojením mezizávitové kapacity už to asi platit nebude.