Jste zde

Smrtící exponenciála a charakteristiky diod

Ing. Robert Láníček, 22. Duben 2020 - 8:30

Když Evropa byla ještě v pořádku a epidemie byla jen vzdálená kuriozita v Říši středu, promítnul jsem studentům pro ilustraci exponenciální charakteristiky diody video. Je v něm pěkně vidět co s tvarem křivky udělá dynamicky měnící se měřítka os. Prahové napětí vyšlo někam na 24. ledna. Já jen doufám, že se graf brzo překlopí do výstupní charakteristiky tranzistoru následované tunelovou diodou ale bez jejího zakončení druhou vlnou.

Video najdete na Youtube.

S grafy se hodně švindluje volbou počátku os, měřítek os, případně se jen vykreslí křivka bez bodů, takže se neví, jestli se prokládá nějaká relevantní závislost nebo jen chaotické souhvězdí bodů podle přání autora. Nemluvě o tom, že body se s výjimkou korekční křivky nespojují ale prokládají, dříve křivítkem a dnes vložením spojnice trendu. Bavíme se samozřejmě o normálních x/y grafech a ne powerpointových nesmyslech nakrájených 3D dortů. Exponenciála je asi nejkrásnější funkce vůbec a v technice se s ní setkáváme velmi často. Kromě zmíněné charakteristiky diody, kde otevírání popisuje Shockleyova rovnice PN přechodu, tak jsou to přechodné děje v RC a RL obvodech, ale exponenciály platí i při ohřevu a chladnutí materiálu. Ve fyzice se exponenciála vyskytuje při radioaktivním rozpadu, ale i při průchodu záření hmotou a přepokládám, že by se určitě našla i v chemických reakcích. Podle oboru se definují časové konstanty, poločasy rozpadu či polovrstvy. U diody se uvádí prahové napětí a to moc přehledné není. A pro zajímavost exponenciální růst může být i nefyzikálního charakteru, jen že to věštění ze skleněné koule autorovi kdysi tak pěkně vyšlo.

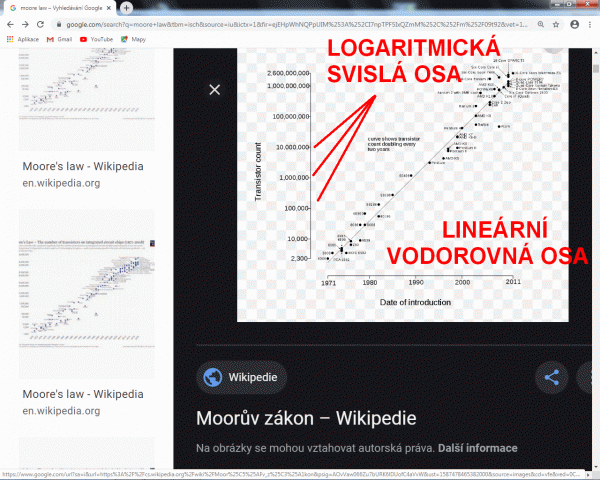
Spoluzakladatel Intelu Gordon Moore v roce 1965 odhadl exponenciální vývoj v elektronice a předpověděl, že počet tranzistoru na čipu se každých 18 měsíců zdvojnásobí při zachování stejné ceny obvodu. A zhruba to těch 55 let platí. A hlavně je to znázorněno ve správných souřadnicích. Je-li svislá osa logaritmická a vodorovná lineární, tak se exponenciála zdeformuje do přímky. A je to snadno kontrolovatelné na rozdíl od všelijakých křivek v lineárních osách je totiž přímka na první pohled jasná. Koneckonců vliv měřítek na osách na tvar křivek byl dobře patrný, už když jsme simulovali charakteristiky svítivek (LED).

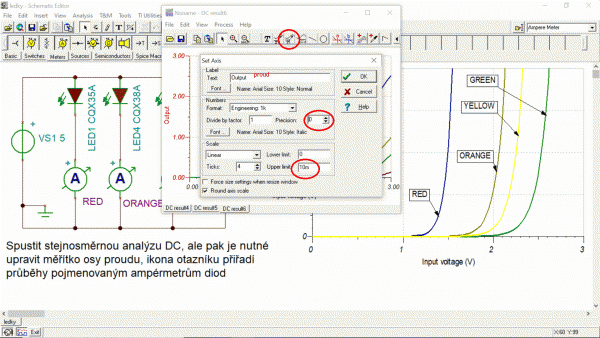
Je pěkné, že na stránkách gymnázia v Klatovech si barevné diody můžete vzdáleně odměřit. Tak zkusíme třeba červenou LED a porovnáme pak se simulací. Mimochodem vzdálená laboratoř se dá ovládat i z tabletu a není potřeba počítač. Myší či ikonami šipek se nastavuje výkon zdroje v procentech a měří se napětí na diodě a nepřímo přes úbytek na odporu proud do diody. Současně se rozsvěcuje ledka zvolené barvy, je to pěkné. Je tam volba vykreslení bodů grafu a případně i export tabulky do formátu programu Excel. Jednodušší je ale tabulku označit myší a okopírovat do schránky a pak vložit třeba do textového editoru Word. Pak už stačí okopírovat jen dva sloupce napětí a proudu a vložit do programu Graph. Prokládající křivka by měla být exponenciála, ale tentokrát možná pro malý počet bodů mi to program Graph nedovolil, takže jsem alternativně vybral mocninou křivku, která vyhověla dobře. Na stránkách k experimentu je pěkně podaná teorie včetně Shockleyovy rovnice respektující i úbytek na vnitřním odporu polovodiče diody (dvakrát podtrženo) a to nemají ani na wikipedii. Pak následuje známé zjednodušení na tvar, kdy se zanedbá jednička zajišťující průchod exponenciály nulou. Teprve v tomto tvaru se to snadno upravuje a dá se pak zlogaritmováním vyjádřit napěti na diodě a derivací pak i dynamický odpor, což je u tranzistoru vstupní odpor (h11=0,026/Ib).

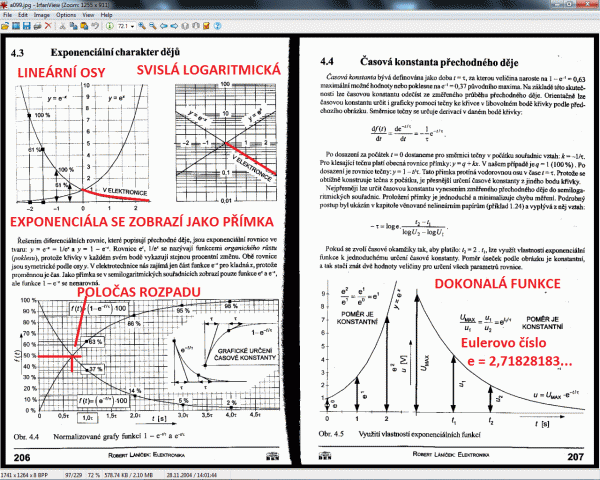
rovedení úlohy lze vytknout jen necitlivost ampérmetru pro stav, kdy se dioda ještě nedostala do kolena charakteristiky. V úvodním obrázku z programu Multisim je zvýrazněno kurzorem, že když dioda není otevřená před kolenem charakteristiky, proud ji prochází. A proud narůstá přesně podle exponenciální diodové rovnice (to jsou ti první pacienti, než to vypukne). A protože měřicí aparatura gymnázia nemá dostatečnou citlivost, aby ukazovala desítky mikroampér a zaokrouhluje to všechno na nulu. Naopak při větším proudu diodou je exponenciální charakter nárůstu potlačen a převažuje úbytek napětí na vnitřním odporu polovodiče. Nebo ještě jinak, v oblasti, kde dioda téměř nevede, se chová jako teoretická exponenciální dioda a když už vede tak je to spíš lineární součástka. Dobře se to posoudí, když se graf diody nakreslí jak do lineárních souřadnic a do souřadnic se svislou logaritmickou osou.

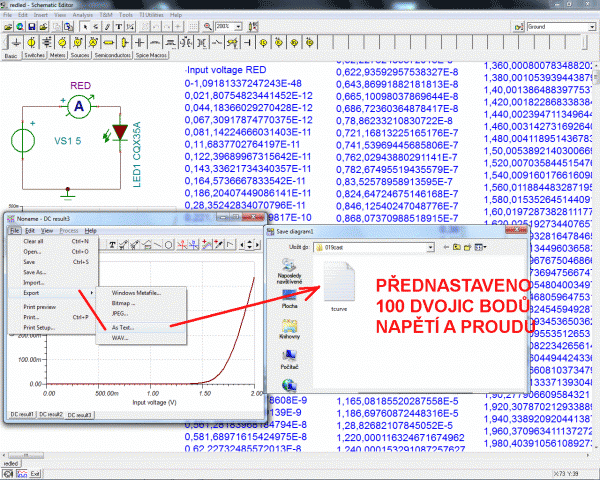
Odsimulované závislosti v programu TinaPro lze exportovat jako tabulku ve formátu textového souboru. A ten lze načíst do libovolného tabulkového procesoru a já dávám přednost programu Graph. Po nakopírování do tabulky posloupnosti x/y je zapotřebí umazat první dva řádky, aby se mohla závislost vykreslit.

A teď přijde ta záludnost exponenciály. To co vypadá jako konstantní nula v lineárních osách a co vzdálená laboratoř vyhodnocuje při měření rovněž jako nulu, žádná nula není. A při zobrazení v logaritmických osách je vidět, že je to naopak exponenciální nárůst proudu stotisíckrát při změně napětí o pouhý volt. A naopak co se většinou považuje za prudký exponenciální nárůst po překonání kolena a otevření diody je už jen lineární nárůst proudu ve shodě i s ukradnutým retroobrázkem. Takže počátecní březnové vtípky: jé tři nakažení, všichni umřeme, mne moc nebavily.

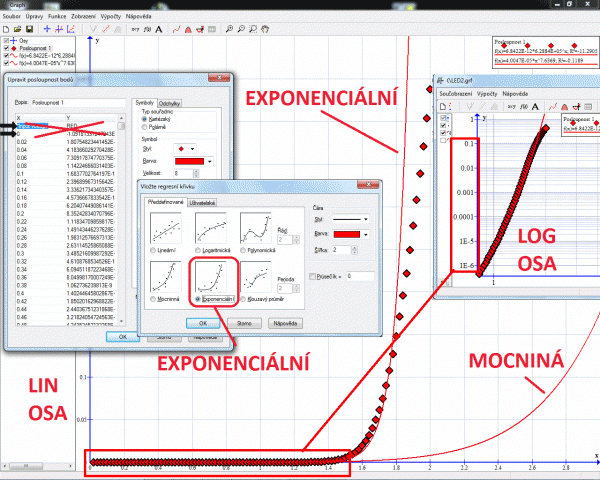
Další otázka je jak určit prahové napětí. Při simulaci jsme se dostali do hodnot proudu (0,5A), kde LED svítit určitě nebude. Protažením téměř dokonalé přímky (R^2==0,9967) vychází prahové napětí 1,7V. Většinou se uvádí u červené diody 1,6 nebo 1,65V. Nejobvyklejší řešení je protáhnout spojnici jmenovitého proudu a desetiny jmenovitého proudu diody.

V rámečku uvnitř obrázku je vidět stejně jako u Moorova zákona vhodnost použití logaritmické svislé osy, protože exponenciála se zobrazí jako přímka. Nejjednodušší model diody připomíná model cívky. Je složen z ideální diody popsané diodovou rovnicí v sérii s odporem polovodiče. A samozřejmě s odporem polovodiče simulační programy počítají.

A vůbec nejčastější exponenciálou a s velmi jednoduchou rovnicí je exponenciální pokles. Podle této rovnice se vybíjí kondenzátor, chladne těleso, klesá radioaktivita, proniká ionizující záření hmotou atd. A opět se exponenciální pokles v grafu s logaritmickou svislou osou zobrazí jako přímka. No a na závěr pro odlehčení jedno fake video s žárovkou. Je to varianta na přenos energie vysokým napětím ala rozvodná soustava. Žárovka je poctivá edisonka, která opravdu hřeje a ne létající ledka se zanedbatelným příkonem. A když se napětí zvedne na kilovolty, stačí pak malý proud pro přenos (P=U*I). A malý proud může téct tenkým drátkem, který je téměř neviditelný.