Jste zde

Princip aktivních reproduktorových výhybek

Ing. Robert Láníček, 8. Duben 2020 - 11:15

Věřili byste, že hrdina hardwarové revoluce Bob Widlar byl jeden čas autorem většiny typů vyráběných analogových obvodů? Jeho jméno nese i jedno ze základních zapojení v integrovaných obvodech-proudové zrcadlo (Widlar current source). A protože to byla šedesátá léta minulého století, tak se traduje i řada historek. Asi nejznámější je, jak ve svém autě přivezl ovci, aby spásala trávu před budovou firmy.

Tenkrát se totiž manažeři nadnárodní firmy rozhodli šetřit a vyhodili zahradníka. Náhodou tam byl novinář, který otiskl článek o úsporách s fotkou ovce před průčelím National Semiconductor. Bob pak zašel asi i s ovcí do baru a dal výpověď. To je scéna jak z filmu Slavnosti sněženek. Nenašel jsem bohužel nikdy žádné video a i těch pár odkazů, co jsem měl, už nikam nevedou. Ale můžete si alespoň koupit plakát s hrdinou

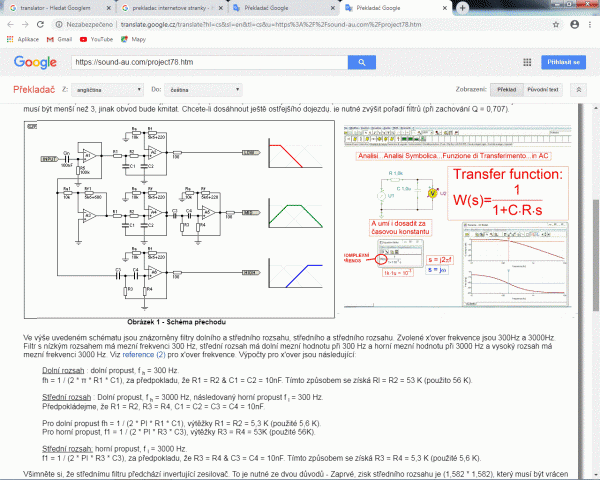
A vrátíme se zpět k výhybkám. Kromě klasické koncepce, kdy jsou na výstup výkonného zesilovače připojeny výhybky a součástí filtrů jsou impedance reproduktoru, se to může otočit. Nejdříve se v nízkoúrovňové části signál rozdělí filtry DP, PP a HP na jednotlivá pásma, přibližně na dekády a výkonový zesilovač bude mít pak každý reproduktor zvlášť. V době levných integrovaných zesilovačů to dává větší smysl, než řešit drahé pasivní výhybky. Lze se tak vyhnout použití cívek a zůstat u RC obvodů a v případě potřeby navrhnout i velmi složité propusti vyšších řádů. Příklad aktivní výhybky byl už na uvedeném obrázku článku o programu Electronics Workbench pana Roda Elliotta.

Do obrázku s textem přeloženým translatorem byl vložen výsledek simulace dolní propusti z italské retroverze. Stěžejní je vzoreček pro přenos v červeném rámečku. Je-li komplexní kmitočet s malý, je člen CRs ve jmenovateli zanedbatelný vůči jedničce a pak bude přenos W(s) = 1/1 (20log(1) = 0dB). Naopak při vysokém kmitočtu se v součtu zanedbá jednička a zjednoduší se to na nepřímou úměru W(s) = 1/(CRs). Hyperbola nepřímé úměry se v semilogaritmických souřadnicích zobrazí jako klesající přímka se sklonem –20dB. Operátor s je komplexní kmitočet (s = j*2pif). Když se zlomek rozšíří 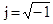, změní se znaménko a bude 1/(j2piRC) = -j/(2piRC). Přenos bude imaginární a orientován na imaginární ose dolů, takže fázový posuv se bude blížit –90°. Důležitý je moment, kdy kmitočet není ani velký a ani malý. Tomuto kmitočtu se říká mezní. A ten nastane, když budou členy jmenovatele stejně velké, tj.1 = CRs. Mezní kmitočet v rad/s je převrácená hodnota časové konstanty RC. Po úpravě s = 1/(RC) a dosazením 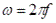bude vzorec pro návrh fmez = 1/(2piRC) anebo jinak R = 1/(2pifmezC). Při mezním kmitočtu je odpor shodný s reaktancí kondenzátoru a bude na nich stejně velké napětí ale posunutá o 90°. Fázorový diagram má tvar čtverce a přenos bude 0,707, což lze určit i výpočtem s pomocí Pythagorovy věty (velikost ve jmenovateli). Posuv fáze bude –45° u integračního nebo+45° u derivačního článku. Pro kontrolu dosadíme do fmez = 1/(2piRC) z obrázku pro zvolený mezní kmitočet 300Hz a použitý kondenzátor 10nF vyšlo 53kOhmů (300 = 1/(2*3,14*53 000*0,000 000 01)

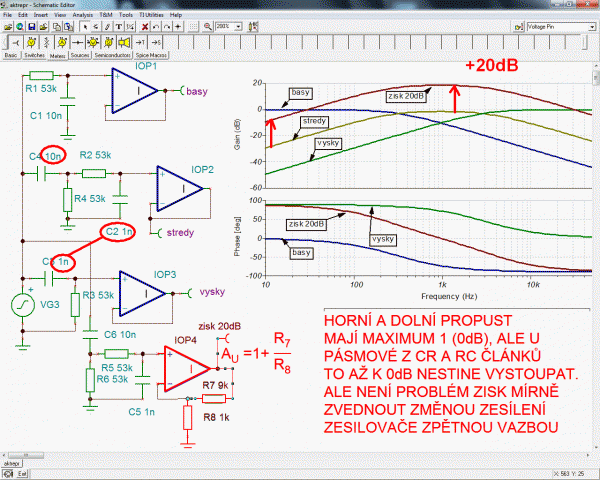
Zapojením dvou RC článků za sebe se získá nejjednodušší výhybka druhého řádu s větší strmostí v nepropustné části. Kvadratická závislost na kmitočtu se v semilogaritmických souřadnicích zobrazí jako přímka s dvojnásobným sklonem +/- 40dB/dekádu a také s dvojnásobným fázovým posuvem +/- 180°.

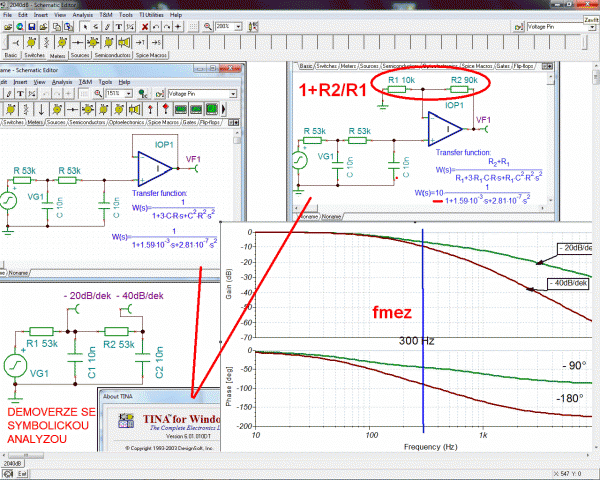
Do schématu dolní propusti druhého řádu odsimulované v TinaPro TI byly jako bitmapy vloženy výsledky symbolické analýzy získané v anglické demoverzi TinaPro6.01.010DT, která stejně jako retroitalská verze uměla symbolickou (symboly) a semisymbolickou analýzu (s dosazením hodnot součástek). Ve jmenovateli je vidět, že komplexní kmitočet s je opravdu na druhou. Navíc vpravo nahoře je ilustrována zpětná vazba nastavující zesílení desetkrát, to je ten posuv o +20dB v předchozím obrázku. Křivky filtrů mohou mít v oblasti průchodů mezním kmitočtem různý tvar. V teorii filtrů se tomu říká aproximace a je pojmenována po jejich autorech (Bessel, Čebyšev, Butterworth, Cauer…). A jsou speciální programy pro návrh filtrů, nebo to bývá i součástí simulačních programů. U výhybek se nejčatěji používa Butterworth s plynulým přechodem a poklesem přenosu o 3dB při mezním kmitočtu. Výkon je kvadratickou funkcí napětí 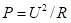a když se umocní zmenšení napětí při mezním kmiitočtu na 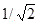tak budou hrát současně oba reproduktory polovičním výkonem a celkový výkon, ale ani impedance soustavy se přitom nebude měnit.

Příště odsimulujeme výkonové poměry na reproduktorech. TinaPro má totiž v sadě přístrojů i wattmetry. Nicméně s výkony to nebývá při simulaci úplně jednoduché kvůli častým chybám při přepočtech amplituda/efektivní ve vzorcích, kde jsou kvadratické závislosti. No a na závěr ještě myšák doporučuje stránky digitálního archivu internetu archive.org. V některých časopisech lze listovat i prezenčně jako v opravdové knihovně.