Velmi pěkně je historie reproduktoru vysvětlena na stránkach edisontechcenter.org. Riceův reproduktor byl už dnešního typu s kuželovou membránou jen princip byl naruby, tj. membránou pohyboval magnet v mohutné pevné cívce.

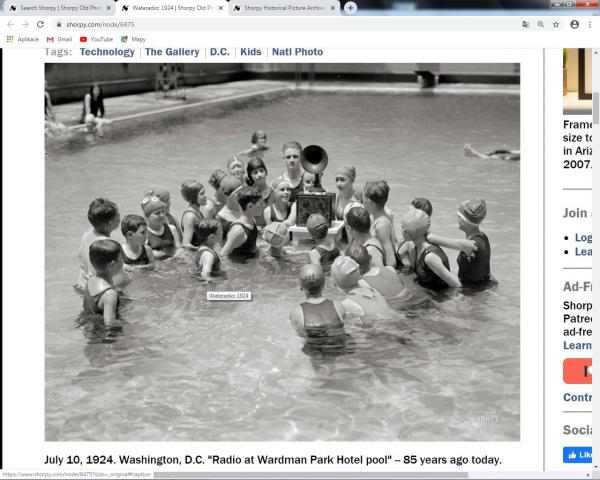
Každopádně tyto elektroakustické měniče jsou nádherné a osobně si myslím, že tvar rohu Magnavox z roku 1920 je dokonalé umělecké dílo. A i ten už měl elektroakustický měnič. Na mých oblíbených stránkách shorpy.com je třeba ozvučení bazénu v roce 1924 zařízením Radiola.

K úspěšnému vyřešení hlasité reprodukce byl zapotřebí zesilovač a tedy vynález zesilovací triody (audion, Lee de Forest 1906). Nicméně se vrátíme k reproduktorovým výhybkám. Použití aktivních výhybek má také svá úskalí a tim je, že v přenosové cestě jsou zařazeny další obvody, které mohou mít negativní vliv na kvalitu reproduktorovaného zvuku. Ale asi stále platí, že nejslabší částí audiořetězce budou reproduktorové soustavy. A ty nejdražší stojí i dnes miliony.

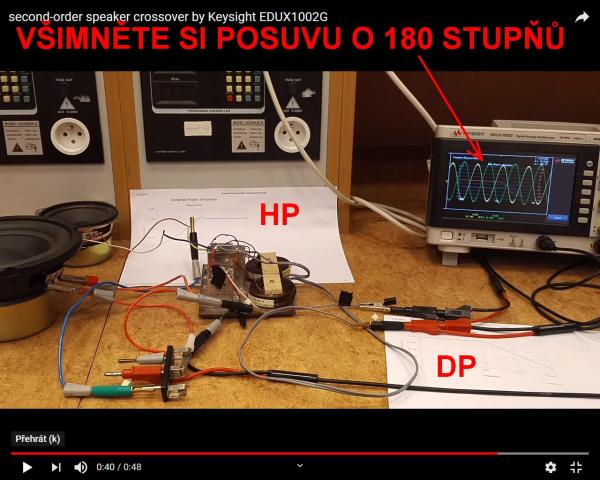
Jsem moc spokojen s osciloskopem Keysight Edux 1002G s jeho možností rychle odměřit přenosové charakteristiky. Logicky by mělo následovat odsimulování charakteristik a asi kdysi i proběhlo a je vytištěno na těch listech papíru na videu. K výhybkám se teď nedostanu a tak neznám hodnoty získané reverzním inženýrstvím (odměřením prvků v zapojení). Výhybky jsou z nějakých prastarých beden a je vidět že kondenzátory jsou typu MP (metalizovaný papír) a cívky jsou vzduchové. Vypadá to na klasické zapojení dvoupásmové soustavy druhého řádu. Na návrh reproduktorových soustav je vhodné použít specializované programy. Mně se líbí LspCAD.

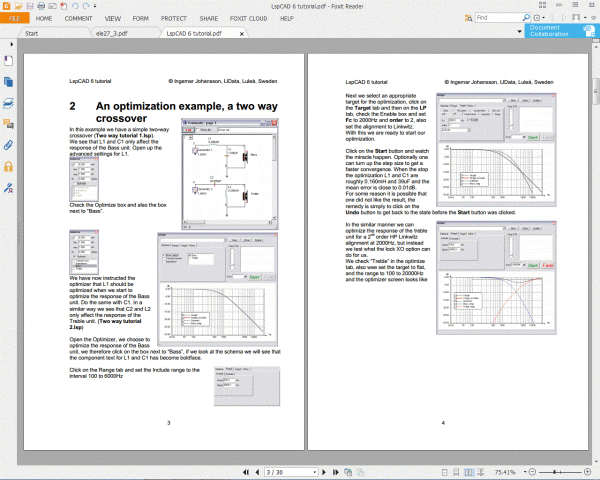
Autor k tomu totiž dodává teoretickou dokumentaci a podrobné návody na příkladech, jak s programem pracovat. Navíc ve starší verzi byly v příkladech i impedanční (*.zma) a frekvenční (*.frd) data reproduktorů, takže jsem si mohl kdysi ověřit, že můj simulační model reproduktoru, tvořený sériovým spojení odporu vinutí a indukčnosti kmitačky s paralelním rezonančním obvodem mechanické rezonance je správně.

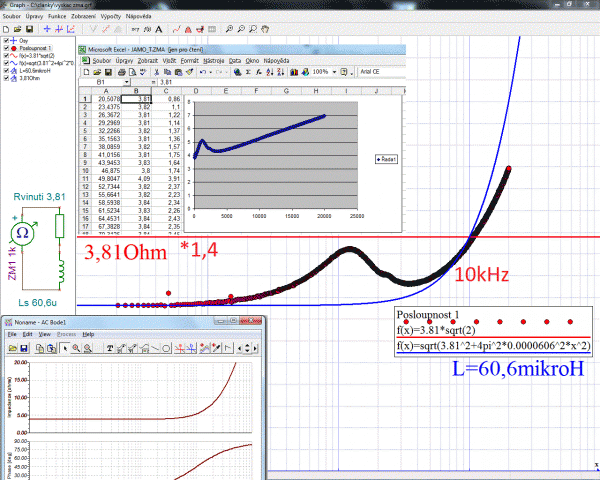
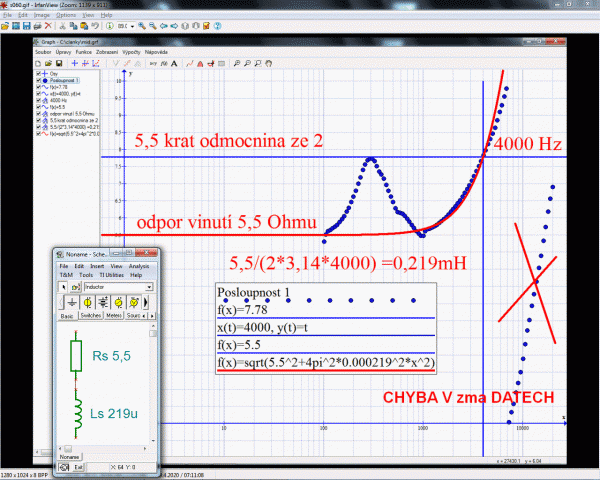
Zma data reproduktorů mají tvar tří sloupců: kmitočet, velikost impedance a fázový posuv a frd data mají kmitočet, SPL úroveň v decibelech a fázový posuv. Nejrychlejší způsob jak z nich vykousnout dva číselné sloupečky vede přes Excel (všechny soubory, export na xtém řádku, oddělovač desetinných čárek je tečka…). Vykreslí se graf XY a v defaultním nastavení v lineárních osách s nepochopitelným šedým excelpozadím grafu a chybějící mřížkou. Je vidět, že výškač se rozhodně nechová jako odpor drátu ale téměř jako čistá indukční reaktance lineárně rostoucí s kmitočtem. Mechanickou rezonanci není třeba uvažovat, protože na rezonančním kmitočtu výškový reproduktor hrát nebude díky horní propusti (výhybce). Známým způsobem, že má-li fázorák tvar čtverce (R=2pifL) bude výsledná impedance úhlopříčkou, tj. 1,4 krát větší se určí indukčnost způsobem naznačeným v obrázku a tedy i náhradní RL model cívky reproduktoru.

Sice to vždycky nakonec nějak dám, ale nemám nervy babrat se s úpravou grafu v Excelu a okopírované dva sloupce kmitočtu a velikosti impedance proto přenesu přes schránku windows  do svého oblíbeného programu Graph. Neumí sice matematické operace v buňkách, ale umí kromě vykreslení grafu z x/y tabulky, také zobrazit funkci a spoustu dalšího včetně derivací či výpočtu určitých integrálů. V obrázku je červeně konstanta pro mezní kmitočet a modře Pythagorova věta pro impedanci z určené indukčnosti z grafu. V obrázku je to rovnice: f(x)=sqrt(3.81^+4pi… Shoda sice úplně dokonalá není, ale vyhoví. Zkontrolovat to jde pak i simulací v programu TinaPro, který má virtuální ohmetr pro vykreslení závislosti velikosti impedance na kmitočtu (v obrázku vloženo vlevo). Indukčnost kmitací cívky se kompenzuje Zobelovým RC filtrem. Odpor je shodný s odporem reproduktoru a opět se to navrhuje na mezní kmitočet Xc=R. Tento sériový RC člen je paralelně k RL cívky reproduktoru. Takže proud bude protékat buď větví RL nebo RC. Celá soustava se pak bude chovat jako by v celém kmitočtovém rozsahu měla pořád stejný odpor a tím pádem samozřejmě i výkon. Jenže to je ale přesněji příkon celé soustavy. A cívkou hýbe proud. Proud je při vyšším kmitočtu zmenšován rostoucí reaktancí a Zobelovým filtrem mu ještě vytvoříme RC bočník, který to málo proudu co zbyde se odvádí RC zkratem mimo reproduktor. Kdysi jsem si jako mladé ucho dopisoval i s panem L. Svobodou, který psal knížky o reproduktorech, že mi to nedává smysl, snad jen, že jsme vykompenzováním indukčnosti z reproduktoru udělali ze soustavy vykompenzovanou činnou zátěž zesilovači.

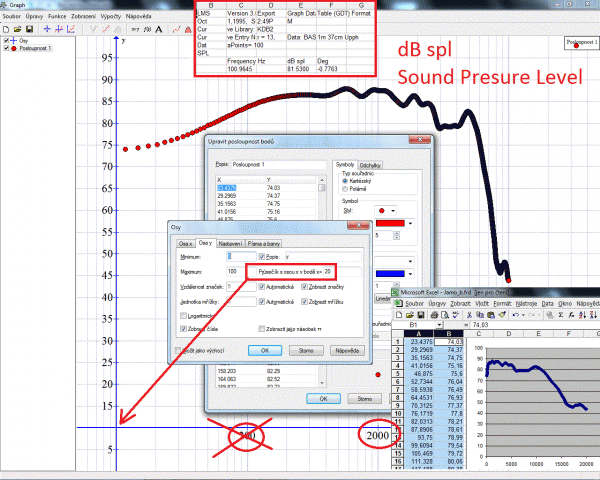
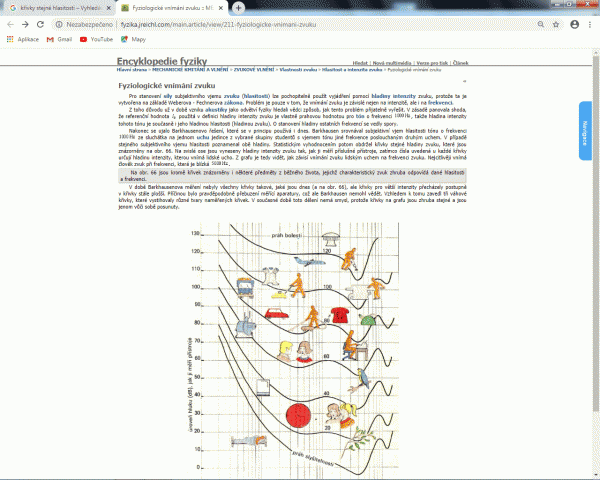
Z obrázku frekvenční charakteristiky z dat *.frd. je vidět, že citlivost reproduktoru je dostatečná, aby to dobře hrálo i tak. V údaji citlivosti Sound Pressure Level je zakódována účinnost reproduktoru, reproduktor se vybudí jedním elektrickým wattem a ve vzdálenosti jeden metr se změří akustická hladina tlaku v decibelech. Je to logaritmická jednotka SPL=20log(p/2*10exp-5), takže klasicky zvýšení tlaku o 6dB je dvojnásobek o 20dB desetinásobek atd. V Excelu je tvar grafu jiný než v programu Graph, protože je vodorovná osa kmitočtu lineární. I jinak dokonalý program Graph má ale chyby, viz obrázek. Když se mu nastaví průsečík s logaritmickou osou na 20, aby byl vidět popisek os, chybně přepíše čísla i na konci dekád. A skoro 90dB SPL reproduktoru je opravdu hodně, když se podíváte třeba na křivky stejné hlasitosti (isofony). Ty bývají často vykresleny špatně, což se pozná snadno. Z definice musí jednotky subjektivní hlasitosti protínat hladiny akustického tlaku na kmitočtu 1kHz. Pěkně i s vysvětlením jak se křivky (fletcher munson curves) měří, to má na svých stránkách pan J.Reichl.

Takže 90 dB z jednoho wattu není zrovna málo, výkonově už to taková sláva nebude, protože akustické hladiny intenzity (watt skrz metr čtvereční) jsou vztaženy k jednomu pikowattu. L=10log (I/10exp-12). Tady je každých 10dB 10krát. Pokud se nepletu (90/10-12= - 3), tak 90dB je intenzita 1mW skrz metr čtvereční. Jinak logaritmy a decibely obzvláště jsou dobrým testem odbornosti novinářů. Třeba před měsícem jsem si se zájmem přečetl článek o nejsilnější siréně na světě, která spouštěla i déšť. Ale…

V původním článku je uvedeno jen 138dB (práh bolesti) a bude to překlep, protože jinak by autor zdroj zamlčel. Ale i tak by se při zapnuté siréně obsluha nerozhlížela po kraji. A bývá to častá chyba, když se autorovi článku nezdá decibelová síla dostatečně velká, tak ji pro jistotu znásobí. Protože 0dB odpovídá výkonově 10exp-12 a každych 10dB výkonových je desetkrát, tak bude: 338/10-12 =21,8 zaokrouhleně raději dolů na 21 řádů, ať je to pěkně po trojicích nul: 1 000 000 000 000 000 000 000W/m2 ve vzdálenosti 30metrů. Můžete si zopakovat i předpony kilo, Mega, Giga, Terra, Exa, Peta a dál to neumím: I=1000PW/m2. Tak záludné ty decibely jsou (teda pokud jsem se nespletl :-). A co teprve ve vzdálenosti 1m? Nejsilnější zdokumentovaný zvuk je asi výbuch sopky Krakatoa, který potrhal ušní bubínky přeživším na desítky kilometrů daleko.

Líbilo se mi uvedení souhrnu vzorečků výhybek na stránkách dexon.cz.

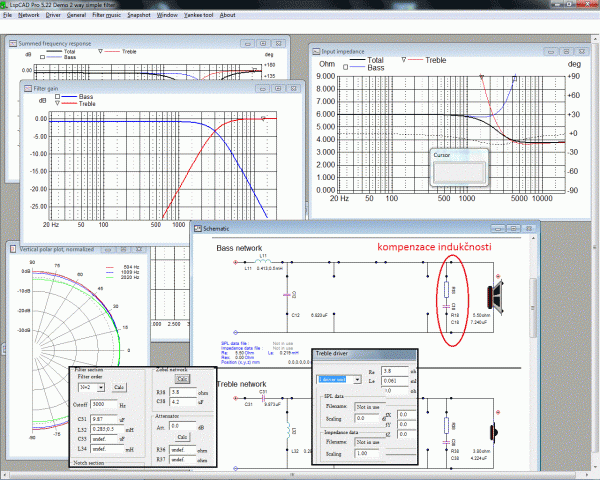
Podle těchto vztahů počítá i jednodušší mód LspCAD starší verze programu, kde je množina pevně daných zapojení a k nim přiřazeny vzorce. Všimněte si jak snadno lze kreslit v programu Graph i svislé čáry pomocí parametrického zápisu funkce. Úsečka 5,5 Ohmů byla překryta funkcí pro velikost impedance, takže není vidět, že elegantně končí (zadá se od do). Tentokrát je proložení odměřených dat dobré sériovou kombinací odporu s cívkou. Takže se zanedbáním rezonance máme dva reproduktory 3,8Ohm/61mikroH pro výšky a 5,5Ohm/219mikroH pro zbytek nf pásma. A tyto hodnoty zadáme do okének programu (driver).

Vpravo nahoře je graf impedance obou částí a celková impedance v závislosti na kmitočtu. Dole je ukázka zadávání parametrů reproduktoru. Může se zadat kromě zjednodušené kombinace odpor/indukčnost i soubor s odměřenými charakteristikami *.zma a *.frd reproduktoru. Frekvenční a impedanční charakteristika konkrétního reproduktoru to samozřejmě celé rozvlní a pak se to může v programu různě kompenzovat a optimalizovat.  Lze přidat útlumový článek, případně zádrž (notch). Postup práce se starým programem v základním módu je jednoduchý. Po zadání reproduktoru se zvolí řád výhybky a případně výpočet Zobel Network a dá se povel spočítat Calc. Vlevo dole si všimněte i předpokládané směrové charakteristiky reproduktoru. V programu je volitelně Advanced režim a vypadá to, že nová verze už ani v jiném nepracuje.  Určitě existují jiné a možná i lepší programy, ale na ukázku jak složitá to může být problematika to stačí. Program samozřejmě podporuje návrh i aktivních výhybek a dokonce i reproduktorových skříní. A předpokládám, že jediná správná reprosoustava schopná zahrát jak sametové basy tak průzračné výšky musí mít pasivní výhybky :-).

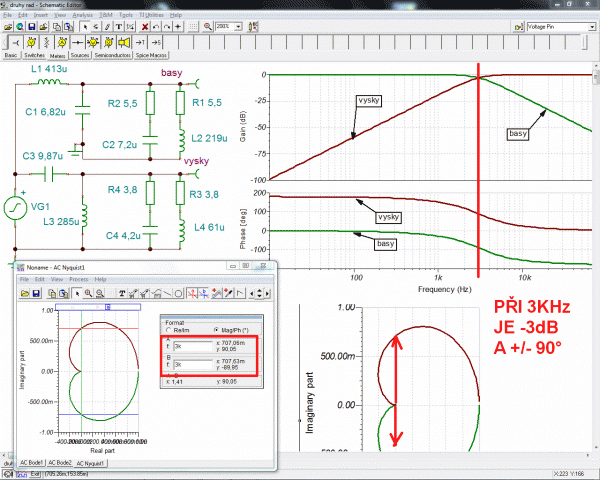
A na ten kardoidní komplexní graf přenosu výhybek druhého řádu s přenosem –3dB při dělicím kmitočtu jsem byl kdysi strašně pyšnej a i myšák to, jak je vidět schvaluje.